前回まで、書籍のサンプルプログラムを動作させてみた。ここでは、ディープラーニングの動作原理の基礎と構成要素を簡単にまとめる。「Deep Learning with Python」本の中では、2章〜4章にまたがって説明されている内容をまとめたもの。
ニューラルネットの計算は一体何をしているかと言うと、「前の層から入力された値の重み付き和を取った後、バイアス項として定数を加える。得られた値に対して何らかの関数 (ほとんどの場合において非線形関数) を適用する」という計算をしている。Pythonのコードで書くと以下の通り。
output = relu(dot(W, input) + b)
各変数はテンソルである。数学の人には怒られそうだけど、実務的にはNumpyの多次元配列と思っておけば良い。inputが入力、Wが重み、bがバイアスを表す。また、関数dotはテンソルのドット積で、reluはランプ関数(活性化関数)を表す。
活性化関数
上記の例では、「relu」が活性化関数。特別な理由が無い限り、隠れ層の活性化関数は非線形関数を用いる。複数の線形演算は合成すれは1つの演算として表現できてしまうため、線形演算を使ってしまうと層を重ねる意味がなくなってしまうから。
Kerasでデフォルトで使える活性化関数は以下の通り。もちろん自分で活性関数を定義することもできるがここでは省略。
- softmax
- elu
- selu
- softplus
- softsign
- relu
- tanh
- sigmoid
- hard_sigmoid
- linear
代表的な活性化関数をプロットしてみた。順不同。スペースの関係で、0以上の値を取るものと負値を取るものを分けている。
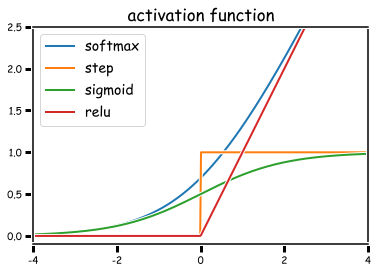
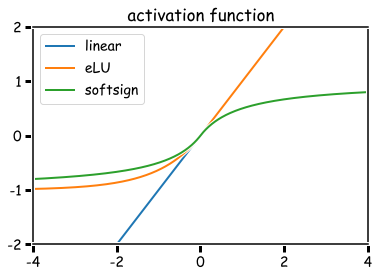
「常にこれを選べば正解」というような万能の活性化関数は存在しないらしい… 何となく、ReLUやtanhはよく使われているのを見かける。ただし、問題によって出力層の活性化関数はある程度限定される。MNIST問題のように多クラス分類であれば、出力層にsoftmax関数を用いる。softmax関数の出力は、全てが正値で総和が1となるように正規化される。つまり、softmaxの出力は、それぞれのクラスに分類される確率として解釈できる。あるいは、Boston Housing問題のように任意の正値への回帰を行う場合は、活性化関数を使用しない(線形関数の層を使う)、など。
ニューラルネット
さて、ニューラルネットのモデル全体の模式図は下図の通り。
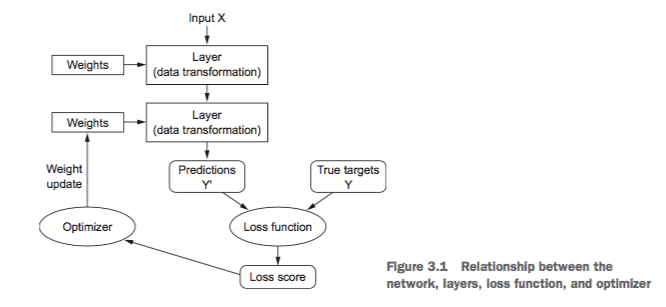
入力Xとそれに対応するターゲット(真の値)Y が与えられる。モデルの演算による予測値Y'と真の値Yとの差を、損失関数 (loss function)を用いて比較し、損失関数の値が小さくなるよう最適化関数 (optimizer) を使って重み(weights) wを更新する。この計算を繰り返して、損失関数の値が小さくなるような重みを選ぶ。
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])
最適化手法と損失関数は、compile時に引数として指定する。それぞれ、引数のoptimizerとloss。また、metricsは評価関数を表し、モデルによる予測の正確さを評価する指標を指定する。損失関数と評価関数は似ているが、評価関数はモデルの訓練のために直接使用される値ではないという違いがある。たとえば、分類問題を評価する「正確さ」は、直接的に最適化することができない値であるので、代わりに交差エントロピーなどの損失関数を最適化することで、間接的に正しい分類を実現する。(p.113)
損失関数 (loss)
損失関数は、どんな基準でニューラルネットの予測の精度を測定するかを定める関数。目的関数 (objective) と呼ばれることもある。どの損失関数も、値が小さいほど予測が正確であるということを意味する。
kerasで使える損失関数は以下の通り。活性化関数と同じく、自分で損失関数を定義することもできる。
- 平均二乗誤差(mse:誤差の二乗和)
- 平均絶対誤差(msa:誤差の絶対値の和)
- 平均絶対誤差率(mspa:誤差の正解値による商(誤差率)の絶対値の和)
- 対数平均二乗誤差(msle:「誤差に1を加えた値の対数」の差の二乗和)
- ヒンジ損失の和(hinge)
- ヒンジ損失の二乗和(squared_hinge)
- バイナリ交差エントロピー(binary_crossentropy)
- カテゴリ交差エントロピー(categorical_crossentropy)
- スパースカテゴリ交差エントロピー(sparse_categorical_crossentropy)
- カルバック・ライブラー情報量(kullback_leibler_divergence)
- ポアソン (poisson)
- コサイン類似度(cosine_proximity)
ヒンジ損失は、予測値と正解値の積について、1以上で0、1以下で 1-x となる関数(同符号であれば損失が小さい)。
交差エントロピーは相互情報量 (2つの確率の相互依存度) とほぼ同じ。分類問題で使われ、分類が正しければ0に、無秩序であるほど1に近付く。
他はあまり分からないのでもう少し調べたい…
最適化関数 (optimizer)
最適化手法も多数存在するけど、結局のところ、全て損失関数の値が減少するように重みを変化させるための手法である。
どの最適化手法も、損失関数の微分 (勾配) の値が少しずつ小さくなるように重みを変化させるという方法を取る。なぜ勾配を小さくするかというと、勾配がゼロの点で誤差関数が極小を取るため。もちろん、極値が損失関数の最小値とは限らない (=局所最適解に陥る可能性もある) し、手法によって収束までの速さも異なる、あるいはそもそも学習が上手く収束しない可能性もあったりするけど、いろいろな要素を考慮しながら最適化できる手法が考案されていて、kerasで使える最適化関数は、sgd, rsmprop, adagrad, adadelta, adam, adamax, nadamというものがある。
ショレさん曰く、「rmspropオプティマイザはどんな問題に対してもまあまあ良いチョイスで、何を使うかそんなに気にしなくてもいい」(p.77) とのこと。別の記事によると、最近はrmspropよりも新しめの(?) adamなどもよく使われるのだとか。