以前に取り上げた3つのサンプルプログラムでは、学習を続けていくと、訓練データの予測精度は向上するものの検証スコアは悪化していった。このように、訓練用データはうまく予測できるものの、逆に一度も入力されたことのないデータに対する予測性能が下がってしまう現象を過学習 (overfitting) と呼ぶ。過学習への対処は機械学習の中心的な課題である。
一般的に、過学習に対して最も効果がある対処法は訓練データを増やすことである。それができない場合は、モデルが保存する情報を減らすことである。
この4.4節では、過学習に対応する方法が記載されている。
ネットワークのサイズ減少
過学習に対する最もシンプルな対処法は、ニューラルネットのサイズ (レイヤー数やノード数) を減らすことである。たとえば、50万ビットのパラメータを持つモデルは、MNISTサンプルの5万個の数字の画像全てに対して、対応した数値を記憶させることができるだろう。しかし、このようなモデルは新しいデータに対しては無力である。このことは常に心に留めておいてほしい。ディープラーニングのモデルは、訓練データのフィッティングに対しては上手く働くことが多い。しかし、真の問題は未知のデータに対する汎化性能の向上である。
一方で、あまりに小さすぎるモデルは、訓練データから有用な特徴量を引き出して記憶することができず、やはり未知のデータへの予測性能は低くなってしまう。この状態を未学習 (underfitting) と呼ぶ。
ディープラーニングのモデルが記憶できるデータの量は、容量・キャパシティ(capacity) と呼ばれることがある。多くもなく少なくもない、ちょうど良いキャパシティを持つモデルを構築するのは難しく、簡単に決められる方法は無い。一般的なワークフローとしては、小さなモデルから始めてだんだん大きくして試していくと良い。
ここでは、IMDBのサンプルに対するモデルをもう一度取り上げる。元々のモデルでは、隠れ層が2層、それぞれが16ノードのモデルを用いた。ここでは、ノード数を4と512に増減させたモデルを用いてみる。
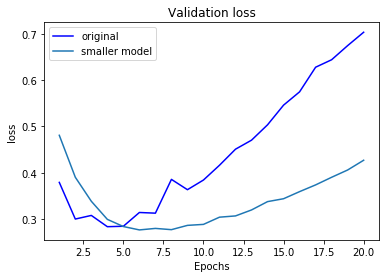
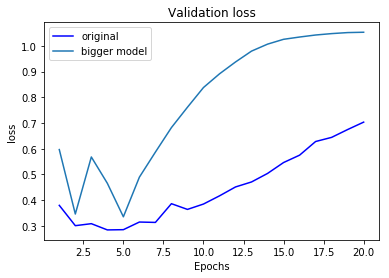
小さいモデルでは過学習が発生し始めるエポックが遅く、また過学習のスピードも穏やかである。一方で、大きなモデルはほとんど即座に過学習が始まっている。
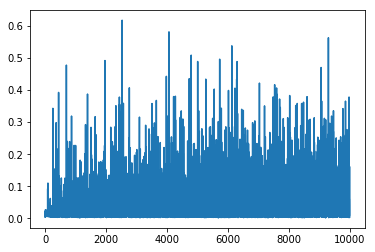
また、訓練誤差を確認すると、大きなモデルでは訓練誤差が即座に減少しその後ゼロ付近で振動している。訓練誤差が即座に減少する状況では、過学習が起こっていることを疑ったほうが良い。(なお、このグラフ、p.107の図4.6は印刷のズレか縦軸の説明が切れてしまっている。これは訓練誤差 (training loss) だと思われる。)
正則化
機械学習では、学習データへの予測に対する何らかの誤差を定式化して、これを最小化するように重み付けを最適化するという問題を解く。しかし、ただ単に誤差関数の値を最小化しようと学習させると、過学習が起こりやすくなってしまう。そこで、パラメータの値の大きさに対して何らかのペナルティを科すことで、過学習を抑えた「ちょうど良い」パラメータを学習させる方法がある。これを正則化と呼ぶ。
抽象的には、これはオッカムの剃刀の原理として説明できる。オッカムの剃刀とは、何かの現象に対する複数の説明があるとするなら、最も前提や仮定の少ないシンプルな説明が正しい可能性が高いという原理である。
機械学習においても同様に、同じ予測ができるモデルならば、シンプルであるほうが汎化性能が高い、と考えられる。
kerasでも以下の2つの正規化が使用できる。
なお、L1正則化はLASSO正則化、L2正則化はRidge正則化、L1とL2両方を使う場合をElasticNetと呼ぶ場合がある。下記はl2正則化を使う例。
from keras import regularizers model = models.Sequential() model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001), activation='relu', input_shape=(10000,))) model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001), activation='relu')) model.add(layers.Dense(1, activation='sigmoid'))
書籍には記載がないけど、正則化については以下の通り説明されることがある。
これを確認してみたい。L1/L2正則化を入れて学習済みのモデルを使う。以前のサンプルプログラムでも用いた、モデル各層の重みを出力する関数を使い、各ノードの重みの二乗和をグラフにしてみる。
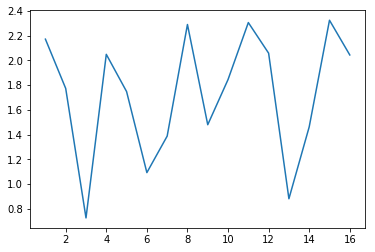
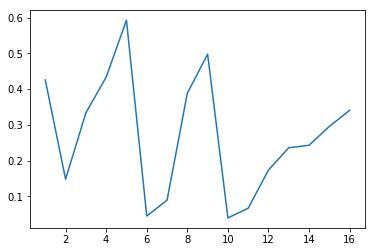

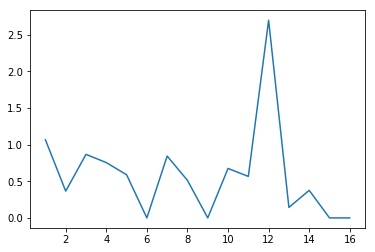
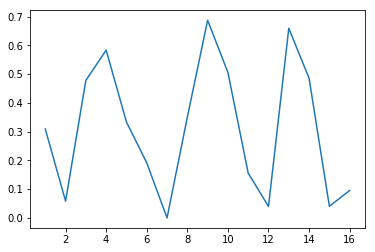
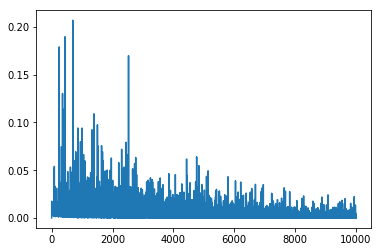


特に最初の隠れ層 (上記のグラフの一番左のもの) を見ると顕著に分かるが、確かにL1正則化の場合はゼロとなったパラメータの数が増えており、L2正則化の場合はパラメータの値の絶対値が減少していることが分かる。(縦軸のスケールが揃っていないので若干分かりづらい…)
最後にドロップアウトを取り上げるつもりだったけど、長くなったので今回はここまで。